Unit 8
Motion on a Fractal
| Download the printable version of this unit in .pdf format (You must have Adobe Acrobat Reader) | |
Sections:
8.1 - Random Walk on a Fractal
8.2 - The Power Law for a Random Walker on a Sierpinski Gasket
8.3 - Diffusion on a Sierpinski Gasket
8.4 - An Exact Solution for the Dimension of a Random Walk on a Sierpinski Gasket
In earlier units we learned about the geometry of branching and fractal objects, how they grow, and how to measure their fractal dimension. But this is only part of the story. Lungs are shaped like natural or random fractals (structures that grow with an element of chance and over a range of magnifications have the same fractal dimension). Some rocks are also shaped like natural fractals. The brain, coral, mountains, bacterial colonies, and the edge of ripped paper towels can also have fractal shapes. But now our question is why ?
Why should the lungs have a branching, perhaps fractal pattern? How does this pattern help the lungs to function better? How does its fractal pattern help coral to grow and thrive? And if mountains are fractal, what are the consequences for water flow? If rocks are fractal, what are the implications for oil or mineral recovery? If a rough surface is fractal, what does that mean for the artist who paints on it? or the hobbyist who runs an electric current through it? Can a subway system whose map is a fractal efficiently serve a city? Can a fractal pattern help things to work better?
An important question for current research is: How do fractal structures improve function? On a practical level, engineers try to understand how water passes through soil and rock in the ground ("hydrological transport properties of porous rock''), the resistance to electrical current on rough surfaces (" electrical impedance of rough surfaces''), or why glass stays hot longer when it is heated than metal does ("thermal transport in amorphous materials'').
How can we simulate a system created by random processes? Two natural fractals grown under the same conditions may have the same fractal dimension, but still be different from one another. No two electrodeposits or snowflakes or root systems or river deltas or lightning strokes or lungs or corals or termite tunnels or city subway systems are the same. So how can we compare members of each group among themselves (such as the branching deltas of two different rivers), and draw general conclusions? If each case is unique, how can we estimate how much oil we can recover from porous rock, how long it takes for a signal to travel through a nervous system, how Nature designs a coral colony for efficient feeding, or how well the human lung exchanges carbon dioxide and oxygen?
|
We start to analyze motion on a fractal by studying a simple system, one which
retains the basic properties of a real system, but which can be easily manipulated
and analyzed. This modeling process helps build our intuition about the behavior
of real objects which have more complicated shapes.
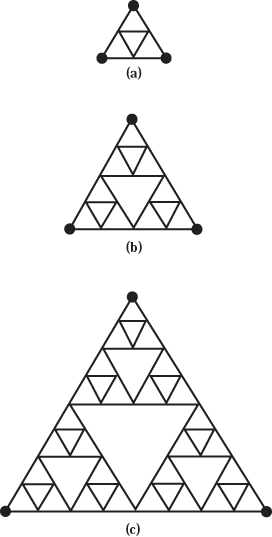 |
The fractal shown in Figure 8.1 is called the Sierpinski gasket and has proved to be a workhorse for testing theories. Because of its simple network connections, many properties of this fractal, such as its fractal dimensions, can be easily found. Do you see that every intersection in the pattern-where two or more lines meet-is connected to four other intersections? Exception: the three external vertices (represented by dots in Figure 8.1), which are connected to only two other intersections in the pattern. Being connected to four other intersections is also true of intersections on a square grid.
|
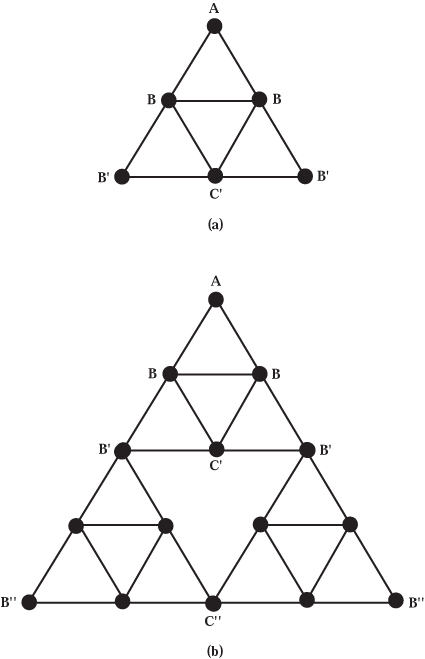
In this unit we begin by reconsidering an exercise we did earlier-finding out
how many random steps it takes on average to travel a given distance
from a starting point. Earlier we studied the random walker on a square grid,
one in which each point had four connections to neighboring points (see Unit
3.7). This was a two-dimensional grid. In this unit
we study what happens if instead you do a random walk between points on a fractal
grid. Specifically, we perform a random walk on a Sierpinski gasket and
find the average number of steps necessary to travel between two points on the
gasket.
After studying the random walk on a fractal, we tackle another kind of problem: How does electricity flow on a fractal? This is analogous to asking, How does water flow through porous rock? or How efficiently will a railway system operate? or What kind of flight network should an airline design to maximize its profits?
 |
Previous: 7.3 - Research Projects