Chelsea High School:

Fractals Investigation

by Kenric Nelson

The Chelsea High School physics class is participating in the Patterns in Nature project with the Boston University Science and Mathematics Education Center and The Center for Polymer Studies.

I introduced fractals with two investigations: Coastlines and Sierpinski Resistor Networks. My goal was to show students that natural objects often have fractal characteristics and that two distinguishing characteristics of a fractal are self-similiarity at different scales and fractional dimension. Three students used the fractals materials for independent investigations.

Coastlines Investigation

Lesson 1: Measuring the Coastline of Nahant

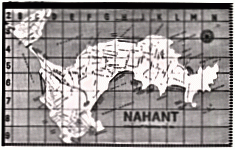
Originally, I planned to have students measure the coastline of their home town of Chelsea, MA. After inspecting several maps, I realized that the waterfront of Chelsea along the Chelsea Creek is a smooth, manmade wharf not a ragged, natural coastline. Close by is the peninsula of Nahant. Nahant's jagged coastline is more interesting for an investigation of fractals.

Using calipers or a pencil compass and a blow-up of a Boston area map, students "walked" around the peninsula of Nahant using different step sizes. Because of the jagged coastline the distance "walked" increases as the step-size decreases. As the data table to the right shows, cutting the step size in half more than doubles the number of steps needed to "walk" the coastline.

The rate of increase in steps taken, can be determined by plotting number of steps versus step size on a log-log graph. The slope of this graph corresponds to the exponential increase in steps as the step-size is reduced. This exponent also corresponds to the fractional dimension of the coastline. If the coastline is smooth, the slope or exponential increase will be close to one - a linear or one-dimensional coastline. If the coastline is extemely jagged the slope or exponential increase will be close to two.

We found that the coastline of Nahant has a fractal dimension of 1.2. This would suggest that the coast of Nahant is not very jagged.

Lesson 2: Using the program Fractal Coastline

Pairs of students working on a Macintosh Color Classics explored the tools of the fractal coastline program. Students were to make a coastline, measure the length of the coastline with different size steps or rulers, graph the number of steps versus step size, and determine the fractal dimension from the slope of the graph. With a little guidance students were able to use the graphical interface and pull down menus of "Fractal Coastline" to complete these steps.

After successfully completing this exploration, we setup a classroom investigation. The coastline is randomly produced based on parameters set by the user. For our investigation all groups set the starting points at three and the roughness at 0.5. Each group used a different number of iterations to make their coastline. Once each group had completed the measuring and graphing of their results, we made a data table of number of iterations versus fractal dimension of the coastline. As the number of iterations is increased the jaggedness of the coastline increases, increasing the fractal dimension of the coastline.

Lesson 3: The Meaning of Dimension

The Coastline Investigation gives students a chance to get their feet wet with fractals. But after completing the investigation many students are still confused about what a fractal is and what the slope of the log-log graphs represents. The meaning of the slope of the log-log graph is clarified by investigating a disc and a line. Students associate these objects with two and one dimensions, respectively. Using the new techniques of plotting number of steps (or number of squares for the the disc) versus step size (or size of square for the disc), and seeing that the resulting slope is two and one respectively gives students a context for the investigation they have completed.

The question 'what is a fractal?' requires students to see and explore alot more examples of patterns in nature. This question is partially answered by the next investigation which explores the sierpinski triangle. Another approach might be to begin with a qualitative investigation of a variety of different natural objects and images. These objects and images could be plants, breaking ocean waves, mountain ranges, ink stains, wrinkled or torn paper. Students would discuss and write down qualitative observations about one or more of these objects. The following questions could prompt their thinking: How does the object fill space? Is its use of space dense or sparse? Are its edges smooth or jagged? What is similiar throughout different parts of the object? What is random or different throughout different parts of the object? How does the whole object, compare with individual parts of the object? What geometric shapes do you see in the object: circles, lines, ovals, spheres?

Sierpinski Resistor Networks Investigation

Building the Sierpinski Resistor Network

Each stage of the project requires different lab groups to complete different tasks: connecting and measuring resistance of each stage of the network, collecting and organizing resistance data. The students were given a table with assignments and instructions for each phase of the project.

Each group started with nine 100 ohm resistors and a circuit board.

Stage One of the Network

Nine lab groups put together a 
stage one network.  The resistance 
is measured from two of the 
outer triangle nodes.  The average 
resistance of the stage one networks 
was 129 ohms.

Stage Two of the Network

Three lab groups collaborated to 
put together a stage two network.  
The average resistance of stage 
two was 213 ohms.

Stage Three of the Network

Finally each groups network 
contributed to the stage three 
network.  The resistance of 
the stage three network was 
378 ohms.

Comparison of Resistor Networks

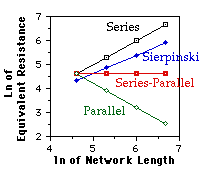
We plotted the natural logarithm of the equivalent resistance versus the natural logarithm of the resistance of one leg of the network. the slope indicates the exponential increase in equivalent resistance for each network.

The series circuit is one-dimensional. The equivalent resistance increases linearly (the slope = 1.0). The series-parallel circuit is two dimensional. The equivalent resistance of the series-parallel is constant (the slope is zero). We are not sure how to define the dimension of the parallel circuit, but its equivalent resistance decreases linearly (the slope = -1.0). The equivalent resistance of the Sierpinski Resistor Network increases at an exponential rate of 0.7609.

In summary, as the fractal dimension of the network increases, the equivalent resistance decrease. As the network increases in fractal dimension more connections exist between the resistors. Each path or connection decreases the networks resistance.

Back to CPS Home Page.